今さら聞けないシリーズ!! 小6・中1数学 おうぎ形の弧の長さと面積で混乱するのはなぜか?その対策をお伝えします。
小学校6年生、中学1年生で、円周、円の面積、おうぎ形の弧の長さ、おうぎ形の面積を求める問題が図形の単元で出題されます。直径×3.14や半径×半径×3.14など公式を覚えられれば、あとは計算を正確にするだけの単元のはずなのですが、おうぎ形になった瞬間に途端に頭を抱える生徒が出現します。
そこで、おうぎ形の弧や面積を求める時に混乱してしまう点は何か。そして、とっておきの方法をお伝えしたいと思います。
おうぎ形の弧や面積を求めるのに混乱してしまうのはなぜか?
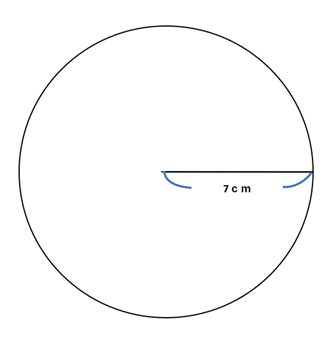
上の図は半径7cmの円だが、円周と円の面積の求め方は次のようになる。
小学生の場合 ◆円周=直径×3.14だから 直径は7×2=14 14×3.14=43.96cm ◆円の面積=半径×半径×3.14だから 7×7×3.14=153.86㎠になる。 中学生の場合 円周率3.14はπで表すことができるため ◆円周=2πr (rは半径)だから 2×π×7=14πcm ◆円の面積=πr²だから π×7²=49π㎠になる。 小学生は、円周率の3.14を掛けなければならないため、 小数の計算が苦手な場合は、時間を要し、また誤答のリスクが高まります。 円の単元が嫌いという生徒は、実は小数のかけ算を不得意にしているケースが 非常に多くなります。 一方中学生になると、円周率をπで表してよいため、 文字の式の計算ルールがしっかりとわかっていれば計算は楽になります。
次は、同じく半径7cmで中心角80°のおうぎ形の弧の長さと面積を求めてみます。
小学生の場合
◆弧の長さ=直径×3.14×$\frac{中心角}{360}$だから 14×3.14×$\frac{80}{360}$=9.77cm(小数第3位を四捨五入)
◆おうぎ形の面積=半径×半径×3.14×$\frac{中心角}{360}$だから 7×7×3.14×$\frac{80}{360}$=34.19㎠(小数第3位を四捨五入)になる。
中学生の場合
◆弧の長さ=2πr×$\frac{中心角}{360}$ だから 2×π×7×$\frac{80}{360}$=$\frac{28}{9}$πcm ◆円の面積=πr²$\frac{中心角}{360}$だから π×7²×$\frac{80}{360}$=$\frac{98}{9}$π㎠になる。
おうぎ形になると、小学生の場合分数の約分や小数への変換が必要になります。 例で出した問題は、中心角が80°のため割り切ることもできず、 かなり複雑な計算が必要となりますが、実は、円やおうぎ形の問題は、 公式自体を覚えられないことよりも、分数の約分でつまづいたり、 小数のかけ算でつまづくことの方が多いのです。
実は、このようなことは、方程式の文章題などでもあてはまり、方程式の文章題ができませんと言ってくる中1の生徒がどこでつまづいているかを分析すると、小5、小6でマスターすべき割合の理解が不十分であるため、式が立てられていないといったものも共通の問題です。
対策法を二つお伝えします。
①左から順番に計算してはいけない!!
半径6㎝で中心角が60°のおうぎ形の面積を求める問題があったとしましょう。
すると、計算式は 6×6×3.14×$\frac{中心角}{360}$ になります。
通常は、36×3.14を計算して113.04 それに$\frac{60}{360}$をかけることになります。 113.04×$\frac{60}{360}$=18.84が答えとなります。
中学生であれば、6×6×π×$\frac{60}{360}$=6πが答えです。
おうぎ形の場合、円周、もしくは円の面積に$\frac{中心角}{360}$をかけることになりますが、360で割るという過程が入ってくるため、これを最後にするのではなく、極力最初の時点で行ってしまうのがポイントです。
6×6×3.14×$\frac{60}{360}$ できるだけ約分して
=6×6×3.14×$\frac{1}{6}$ 半径の6と分母の6が約分でともに1になるため、
=1×6×3.14×$\frac{1}{1}$ となるため、結局6×3.14だけを計算すればよいことになります。
=18.84
分数を苦手とする場合、約分を先にしてしまうという発想と処理が十分にできていない傾向にあります。したがって、しっかりと分数の計算の練習を行うことが不可欠です。
②おうぎ形の面積を簡単に解く方法!!
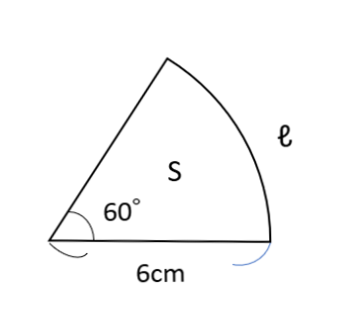
おうぎ形の面積の求め方には、もう一つあります。 それは、おうぎ形の半径をr、この長さをℓの面積をSとすると S=$\frac{1}{2}$ℓr で求まります。
半径6cm、中心角60°の弧の長さは、2×6×π×$\frac{60}{360}$で2πです。
したがって、S=$\frac{1}{2}$2π×6=6πと求まります。
小問①で弧の長さを求めるような問題が出題された場合は、これを利用して簡単に面積を求めることができますので、ぜひ覚えておいてください。








ディスカッション
コメント一覧
まだ、コメントがありません